Como programar um jogo isométrico (2.5D)

TL;DR

Aqui está a função JavaScript para converter um ponto tridimensional em um bidimensional:

function to_isometric(point) {
  const angle = Math.PI / 6; // 30°
  const cos = Math.cos(angle); // ≈ 0.866
  const sin = Math.sin(angle); // = 0.5

  return {
    x: (point.x - point.y) * cos,
    y: (point.x + point.y) * sin - point.z
  };
}

Se você não consegue converter isso para a linguagem de programação que está usando, você não merece ter um design isométrico em seu jogo.

Explicação mais detalhada

Gráficos isométricos eram e são comuns em jogos. Esse estilo oferece uma espécie de mistura entre 2D e 3D que forma um estilo único.

O jogo Sims City é um exemplo de um que usa o estilo de arte isométrica.

O funcionamento do desenho isométrico é por meio de três retas separadas por 60º entre si, onde cada uma representa uma dimensão. Essas retas permitem converter um ponto tridimensional em um bidimensional usando a projeção ortográfica:

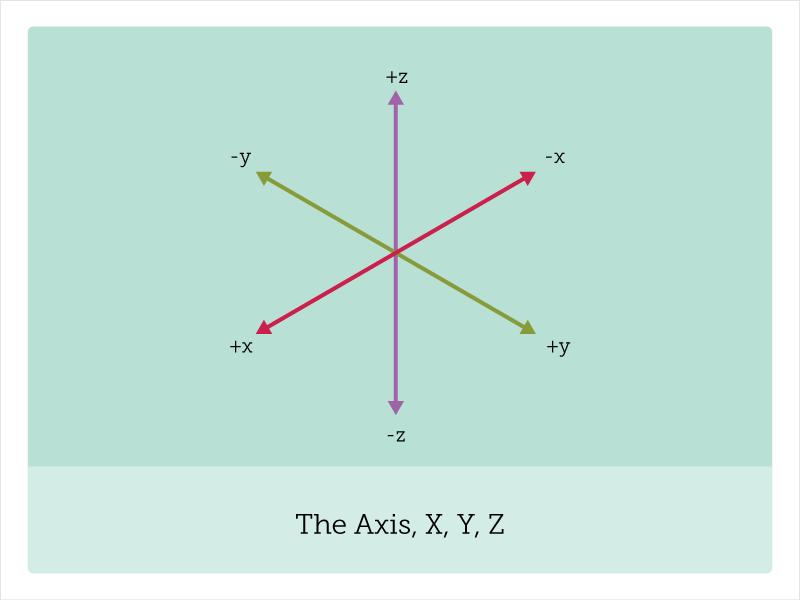
A matemática por trás

No desenho isométrico, como dito, temos três retas separadas por entre si 60º. Entretanto, como o eixo Z é totalmente vertical, vamos focar, por enquanto, apenas na X e na Y:

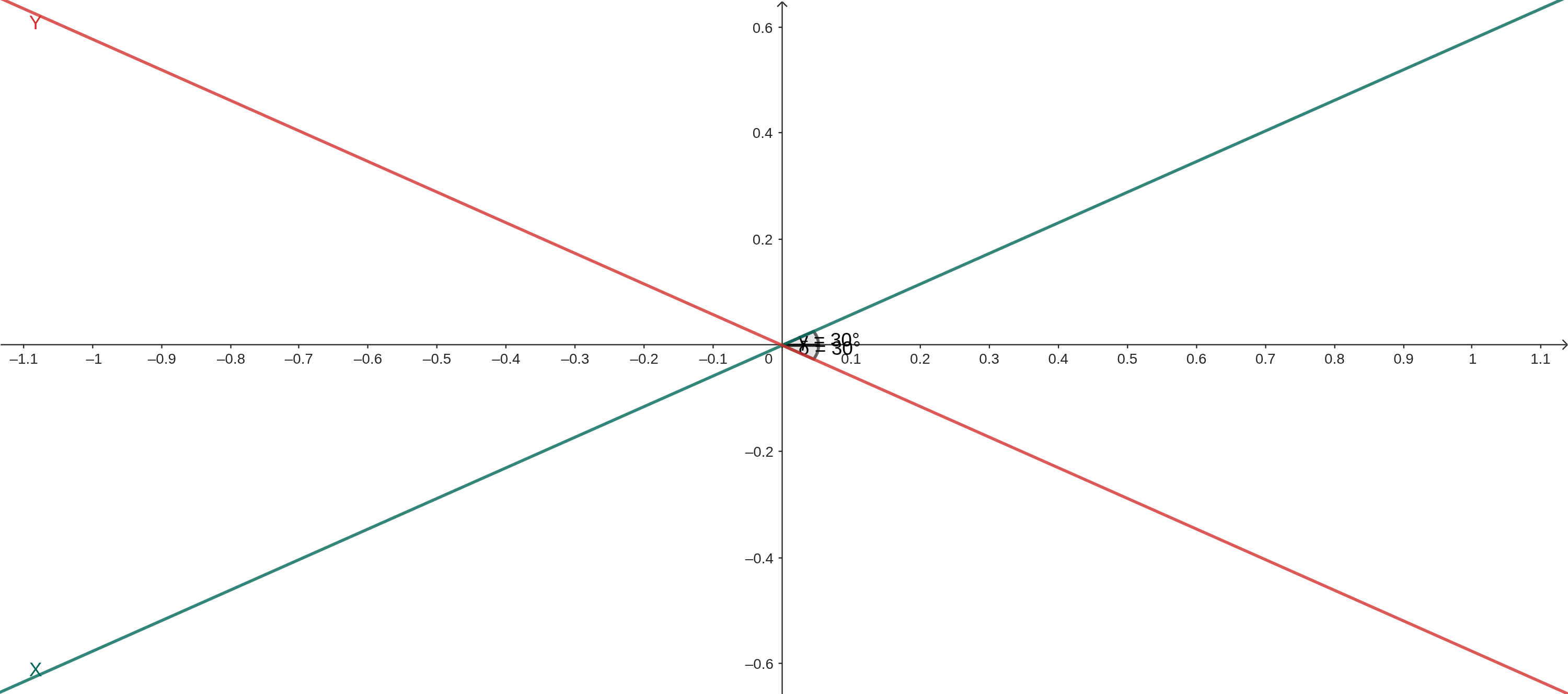
Como é possível observar, os eixos X e Y estão em um ângulo de 30º em relação ao eixo X real (no caso anterior estavam em ângulos de 60º entre si), então a primeira coisa que será feita é encontrar os pontos de cada reta de acordo com a distância da origem – o que pode ser feito com seno e cosseno. Para isso, vamos supor um ponto tridimensional T = (3, 5, 0) (a dimensão Z não será considerada no momento), e queremos encontrar um ponto bidimensional A (que está na reta X) e um B (que está na reta Y):

Calculando A e B:

Plotando os pontos no gráfico:

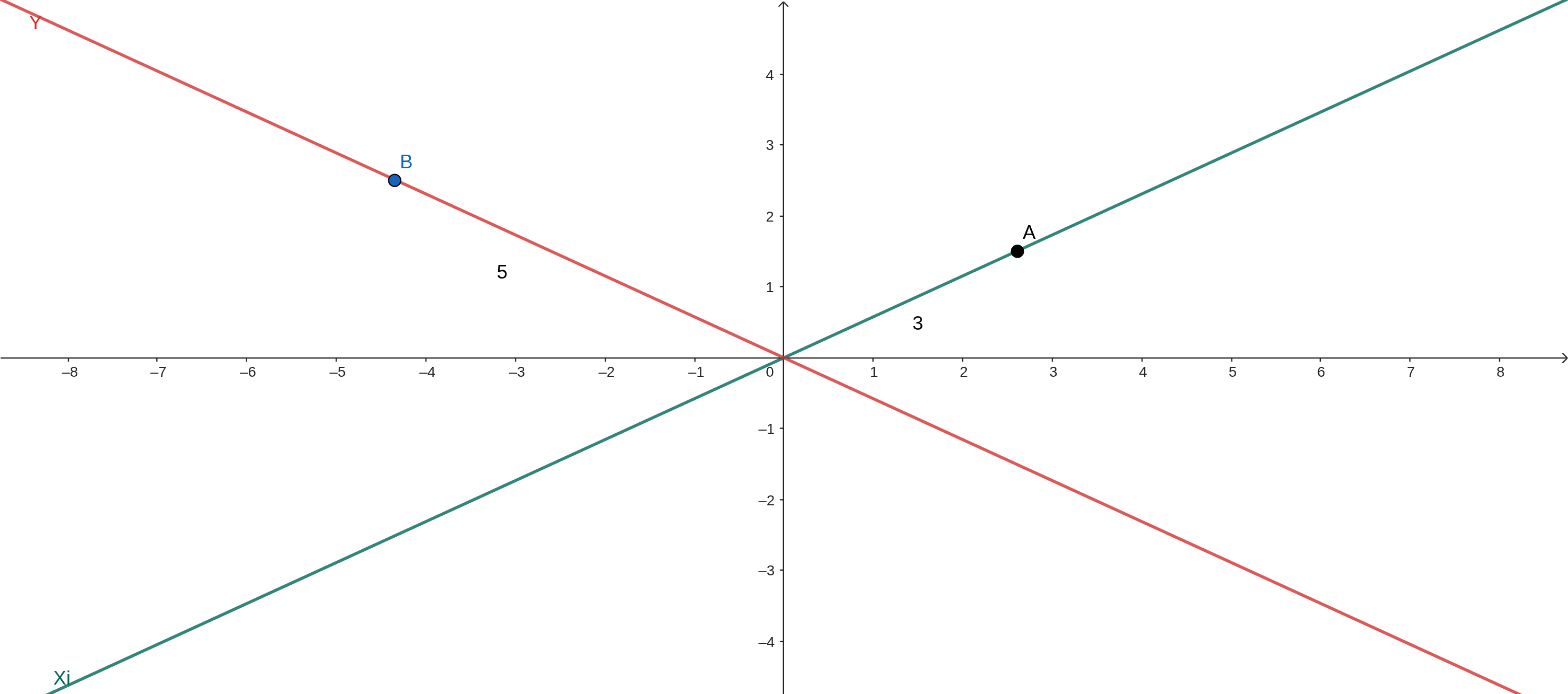
Agora, para sabermos o ponto real R – o que será desenhado na tela – temos que somar os dois vetores:

Plotando no gráfico:

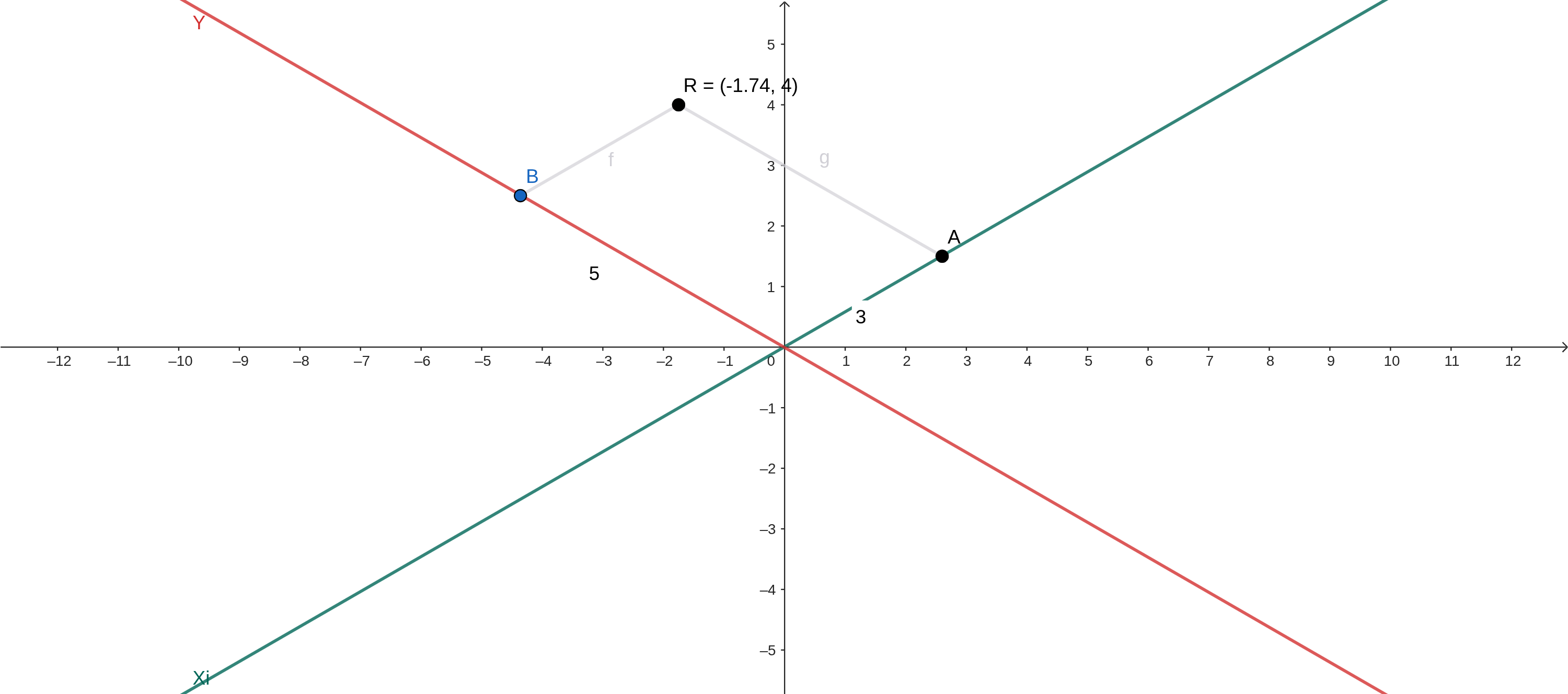
Para adicionar o eixo Z é só somar esse valor ao Y real plotado – já que ele é totalmente vertical –, então se o valor de Z do ponto T fosse 3, o vetor de posição que será desenhado será $\begin{pmatrix} -1.74 \\ 7 \end{pmatrix}$.

Função genérica

Uma função genérica seria dessa forma:

Por que na função JavaScript o Z é subtraído e não somado?

Se você for bem observador, você deve ter percebido isso. O motivo disso é porque na maioria das bibliotecas gráficas (SDL, HTML Canvas, Raylib, p5.js, etc.), quanto menor o valor de Y mais alto fica o ponto – o que é o inverso da maioria dos planos cartesianos, como o do Geogebra, que eu usei para demonstrar o funcionamento. Entretanto, se você estiver usando uma Game Engine como a Unity ou Godot, você deve mudar isso para somar ao invés de subtrair.

Implementando em p5.js

Abrindo editor.p5js.org, tem um editor on-line onde é possível programar em JavaScript usando a biblioteca gráfica p5.js – ela não é uma das melhores pra criar jogos, mas é muito fácil e muito usada para aprender programação.

Inicialmente, vai aparecer um código assim:

function setup() {
  createCanvas(400, 400);
}

function draw() {
  background(220);
}

A função setup roda apenas uma vez, no início do jogo, enquanto a draw roda todo loop. Rodando, vemos apenas isso:

O que queremos fazer é criar uma grade que se movimente como ondas, para isso, vamos usar a função do TL;DR. Depois, vamos desenhar pontos separados igualmente entre si por meio dessa função:

[...]
function draw() {
  background(220);
  
  // Coloca a câmera no centro
  translate(width/2, height/2)
  
  const grid_size=5
  const grid_distance=30
  for (let y=-grid_size; y<grid_size; y++) {
    for (let x=-grid_size; x<grid_size; x++) {
      // Transforma ponto 3D em um 2D
      let drawn_point = to_isometric(
        {x: x*grid_distance, y: y*grid_distance, z: 0}
      )
      
      // Desenha o ponto
      stroke(255, 0, 0)
      strokeWeight(3)
      point(drawn_point.x, drawn_point.y)
    }
  }
}

Assim, o resultado é esse:

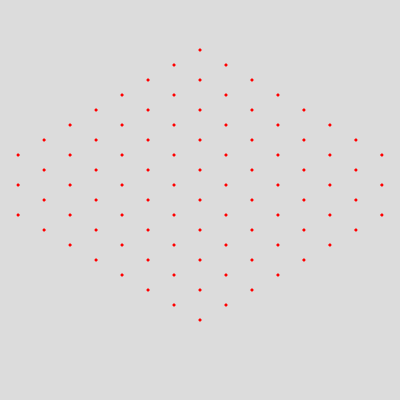
Animando os pontos

Para isso, vamos usar a função seno, que, em um gráfico, se parece assim:

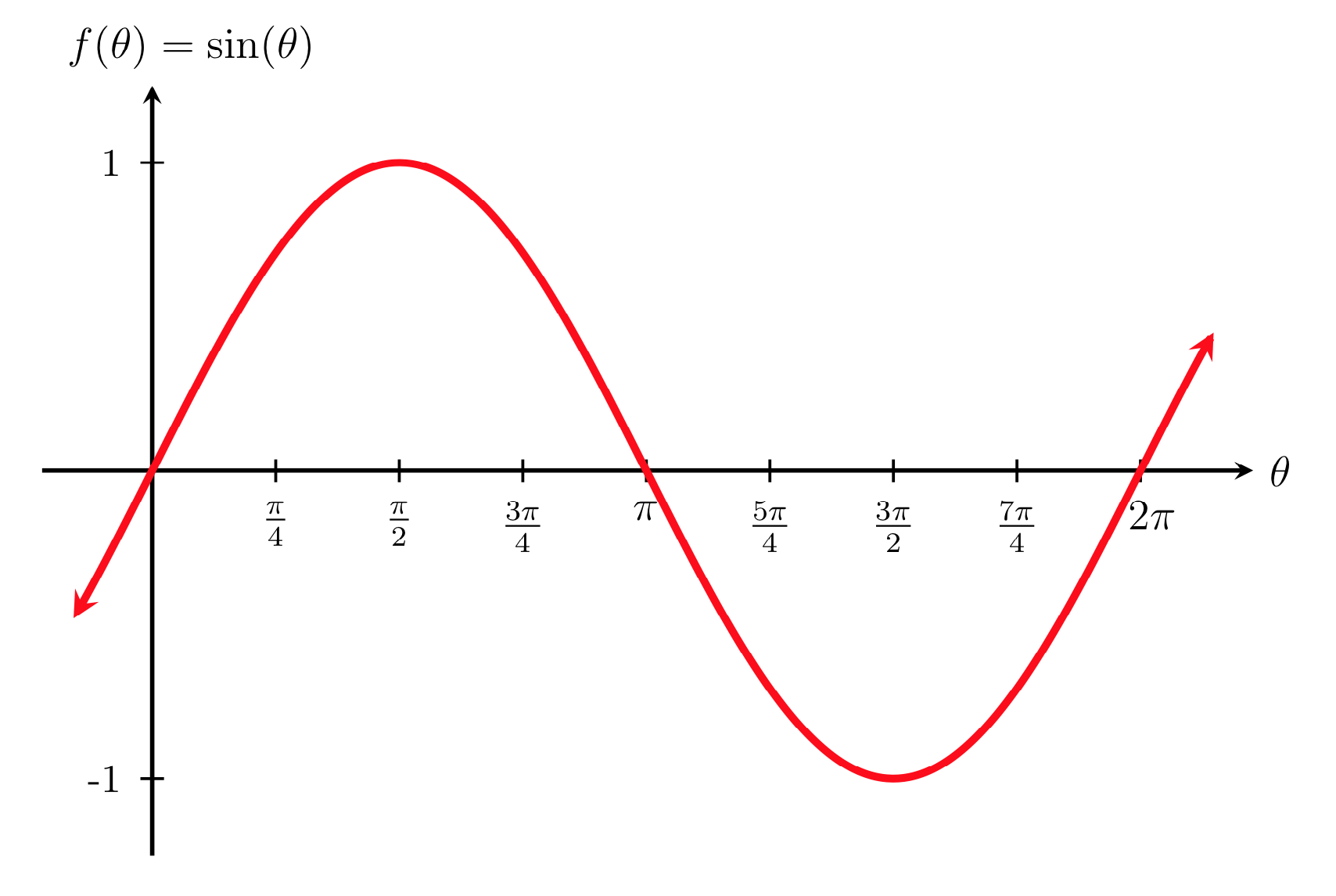
Passando o tempo desde o início da execução do programa para a função, o que pode ser feito pela função millis() do p5.js – que retorna quantos milissegundos desde o início da execução–, podemos animá-los:

let drawn_point = to_isometric(
  {x: x*grid_distance, y: y*grid_distance, z: Math.sin(millis()/1000)*20}
)

Resultado:

Entretanto, como podemos ver, todos os pontos se movem igualmente. Para mudarmos isso, vamos adicionar um valor de offset para cada ponto, definido pela posição Y deles:

let drawn_point = to_isometric(
  {x: x*grid_distance, y: y*grid_distance, z: Math.sin(millis()/1000+y)*20}
)

Resultado:

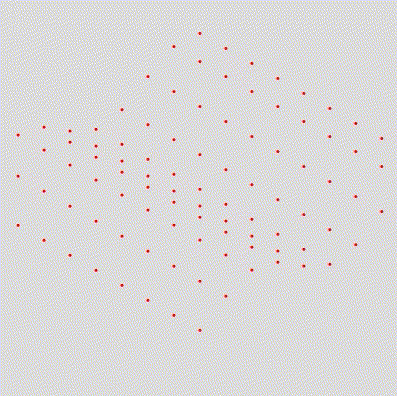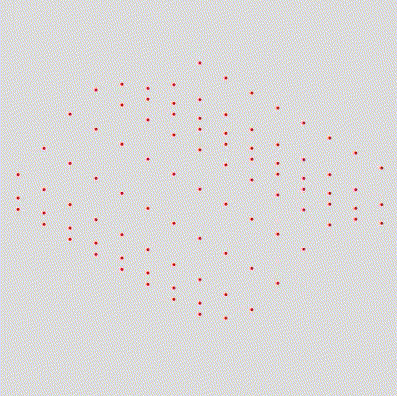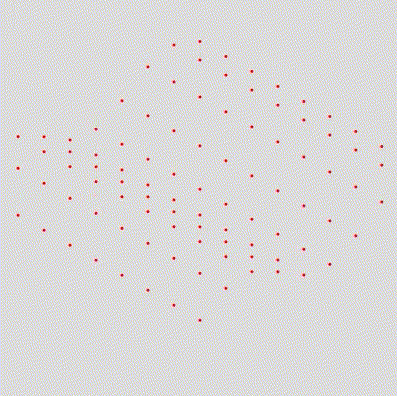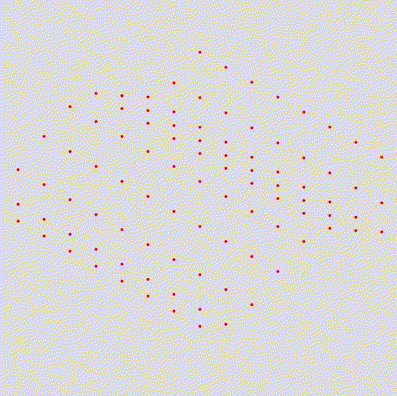
Adicionando sprites

Para isso, eu vou usar esses sprites no opengameart.org. Daí, eu cortei e diminuí a resolução no GIMP de forma que fique apenas um cubo:

Baixe essa imagem e coloque no editor. Para isso, crie uma conta e depois clique na seta no lado esquerdo do editor, daí clique no símbolo de “mais” e em “Upload file”, e selecione o arquivo do cubo.

Para desenhar o cubo, defina uma variável global chamada cube:

let cube

Depois, dentro da função setup(), declare a variável como sendo a textura do cubo:

cube = loadImage('cube.png')

E, ao invés de desenhar o ponto, desenhe a textura, lembrando de manter o tamanho delas como sendo grid_distance vezes dois:

/*stroke(255, 0, 0)
strokeWeight(3)
point(drawn_point.x, drawn_point.y)*/
image(cube, drawn_point.x, drawn_point.y, grid_distance*2, grid_distance*2)

Resultado: